Molecular Spintronics
Magnetic molecules are synthesized for implementation between nano-electrodes to address the interplay between the spin degree of freedom of the iterant electrons with the electronic / nuclear spins of the complexes. Different types of Molecular Electronic devices are constructed in close collaboration with physicists (W. Wernsdorfer, Grenoble; H.B. Weber, Erlangen).
|
Magnetic Surface Coupling |
Spin-split Orbitals |
|
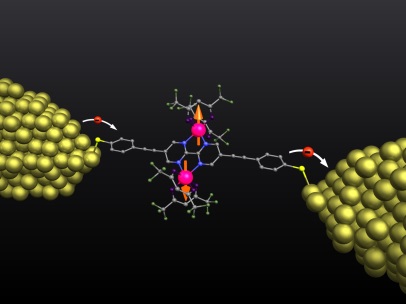
Supramolecular Spin Valves |
Spin Transistors |
Molecules as Quantum Objects
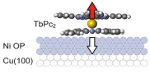
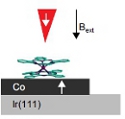
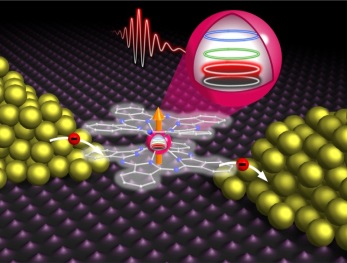
Molecules can be considered as physical Quantum Objects. The use of molecular materials represents the advantage that the active quantum processing elements consist of an atomic core of one-to-few open spin ions surrounded by a shell of organic material. At low temperature such molecular spin objects behave as simple, few-level systems and their spin degree of freedom can be sufficiently decoupled from the environment to achieve long decoherence times and making them to ideal candidates for the implementation of qubits. Since quantum coherence and stable entanglement of electron spins are extremely difficult to achieve, alternative concepts propose the use of nuclear spins (embedded in a controlled organic environment) as quantum information carrier. Nuclear spins are extremely well isolated from environment and less prone to decoherence, and the coherent manipulation can be adapted by tailoring the molecular environment. However, although being well isolated from their surroundings, nuclear spins have to be addressed, ideally electronically since complementary with existing technologies. The delicate balance between decoupling of the quantum object for stable coherence and connecting it for read out can be carried out by synthetic engineering of the molecular components. One example of the successful realization of Molecular Qubit, the completely electronic read out of a coherence of a nuclear spin embedded in a molecule (TbPc2), was recently reported in Science and binuclear metal complexes were proposed for the realization of Molecular Qugates (see Nature Nanotechnology below).
 |
 |