Introduction
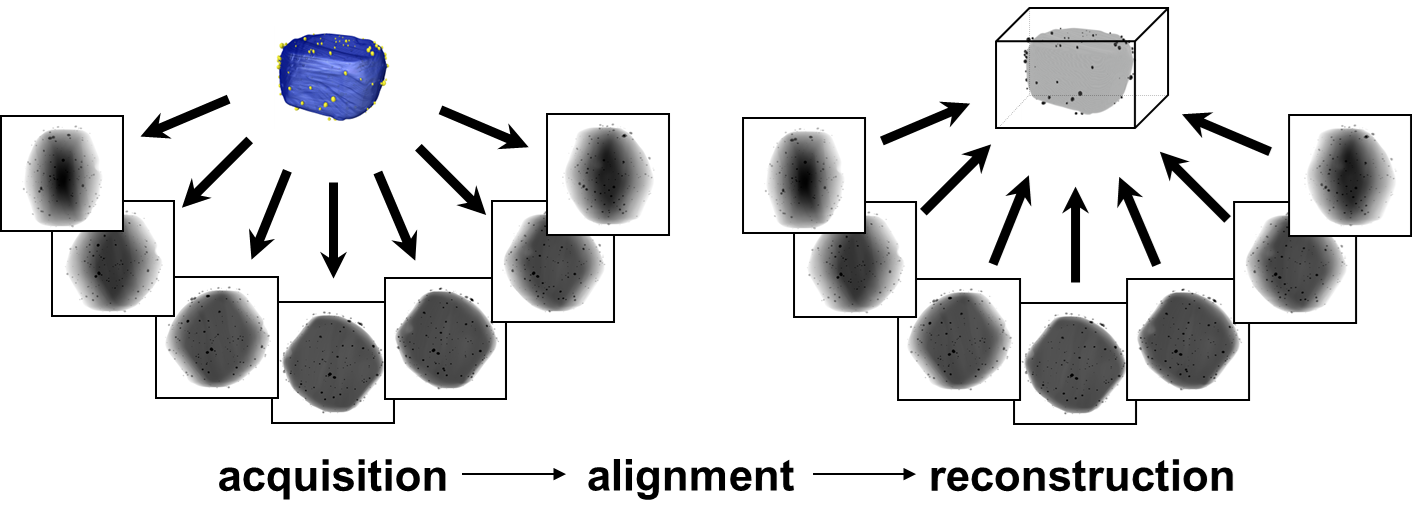
The basic idea of electron tomography is very simple: from a collection of a large number of projections over a wide angular range, it is possible to reconstruction the 3D shape of the imaged object. The basis is the Fourier slice theorem, which states that the Fourier transforms of a projection image corresponds to a central slice of the 3D Fourier transform of the corresponding object. By combining the Fourier transform of each individual projection under the appropriate angle and then performing an inverse Fourier transform one gets the real space structure of the object back (Fig. 2). Alternatively, the reconstruction can be done in real space using direct backprojection appoaches (Fig. 1).
|
Fig. 1: Schematic representation of a tomographic reconstruction: 1) acquisition of projecion images at different tilt-angles, 2) alignment and 3) real space back projection. |
Fig. 2: Schematic representation of a tomographic reconstruction in recipical space: 1) acquisition of projecion images , 2) Fourier transorm, 3) combination of Fourier transform at different tilt-angles, and 4) inverse Fourier transform to reconstruction original shape (from Friedrich et al. (2009) Chem.Rev., 109: 1613). |
Both approaches are equally valid, just different mathematical implementations. However, for the 3D reconstruction to work properly, two improtant aspects have be fullfilled:
1) The projection images have to be true projections of the structure (the signal has to be a strictly monotonic function of the materials density, composition, or whatever property should be reconstructed in 3D ... in practice slight (random) variations can be tolerated in the data, but large systematic differenes are problematic.
2) The tilt-series has to be very well aligned, so that it corresponds to a true rotation around a single axis. The best way to achieve this is an alignment based on fiducal markers using e.g. IMOD or FEI Inspect3D.
Depending on the sample thickness, the electron beam stability and the resolution of the original images, it is typically possible to reconstruct object features at the 1-2 m level in 3D using electron tomography for normal materials science TEM specimens. An estimate for the 3D resolution (d) of a recontruction of a spherical object of diameter (D) based on (N) projections can be obtained based on the Crowther equation
d = pi * D / N
If the tilt-series has only been acquired covering a limited tilt-angle α, all features will be elongated in z-direction, which can be approximated by the elongation factor e
e = SQRT( (α+sinα*cosα) / (α-sinα*cosα) )
Application Examples
We have used electron tomography for a wide range of materials science applications ranging from catalysis, to quantum dots, to polymer composites and semiconductor structures. A few of these examples are shown here to illustrate the potential that electron tomography offers.
|
Fig. 3: Volume rendering of a superlattice formed by CdS quantum dots. The lattice parameters of the cubic lattice were determined to be 3.2 nm. Individual supperlattice defects such as vacancies and dislocations could be imaged in 3D. The 'large' yellow particles are 5 nm gold labels. |
Fig. 4: Surface rendering of a bicontinuous block-copolymers with single layer exfoliated silicates. |
Fig. 5: Surface rendering of a DRAM transsistor. The gate oxide as well as ~1.5 nm oxynitride layers are visible in the 3D reconstruction. |
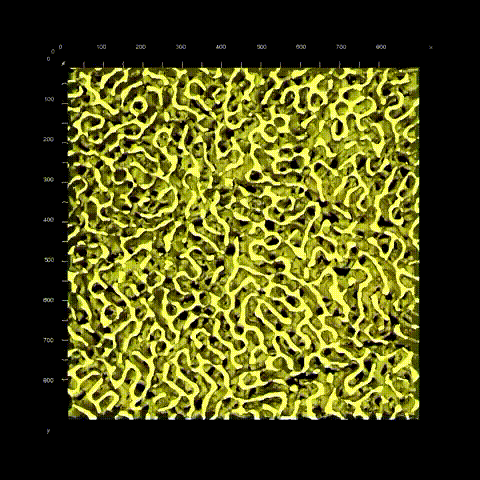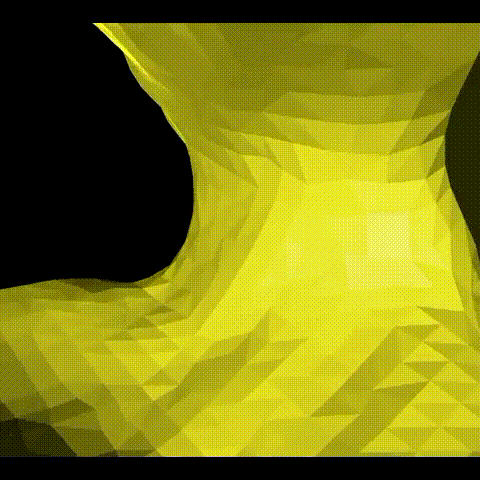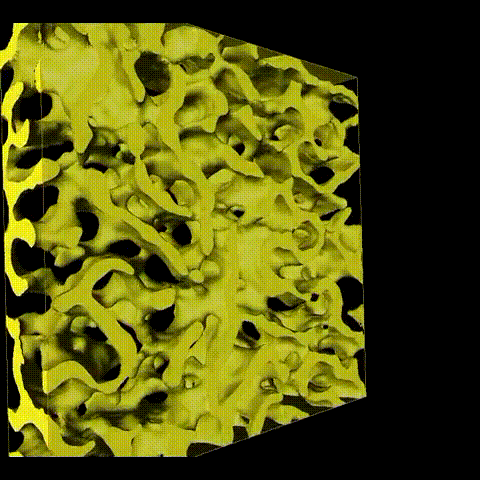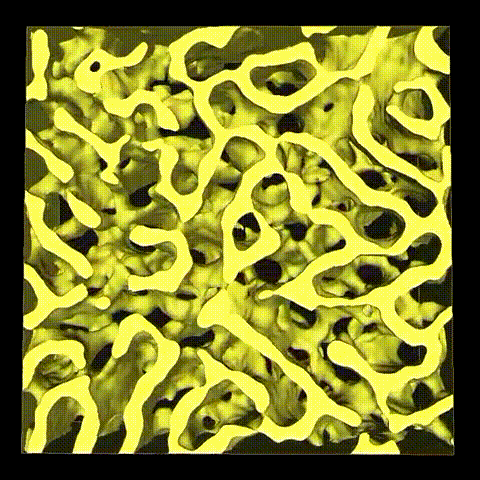
Porous Materials
As an example for a quantitative analysis of interconnected structures, we have been working in close collaboration with Prof. Ulrich Tallareks group at the University Marburg, Dr. Katja Schladitz at Fraunhofer ITWM and Dr. Alberto Villa group at the University Milano on describing the morphology of porous media across length scales from the nanometer to the micron level quantitatively by characterizing both the topology and the geometry based on segmented FIB slice&view tomography and (S)TEM tomography data as illustrated in Fig. 6. Whereas classical bulk characterization techniques such as small angle X-ray scattering or N2/Hg porometry require a model to analyze the pore structure, this approach provides directly interpretable information while covering statistically significant volumes. In fact, this approach be used to develop models for an analysis using bulk techniques.
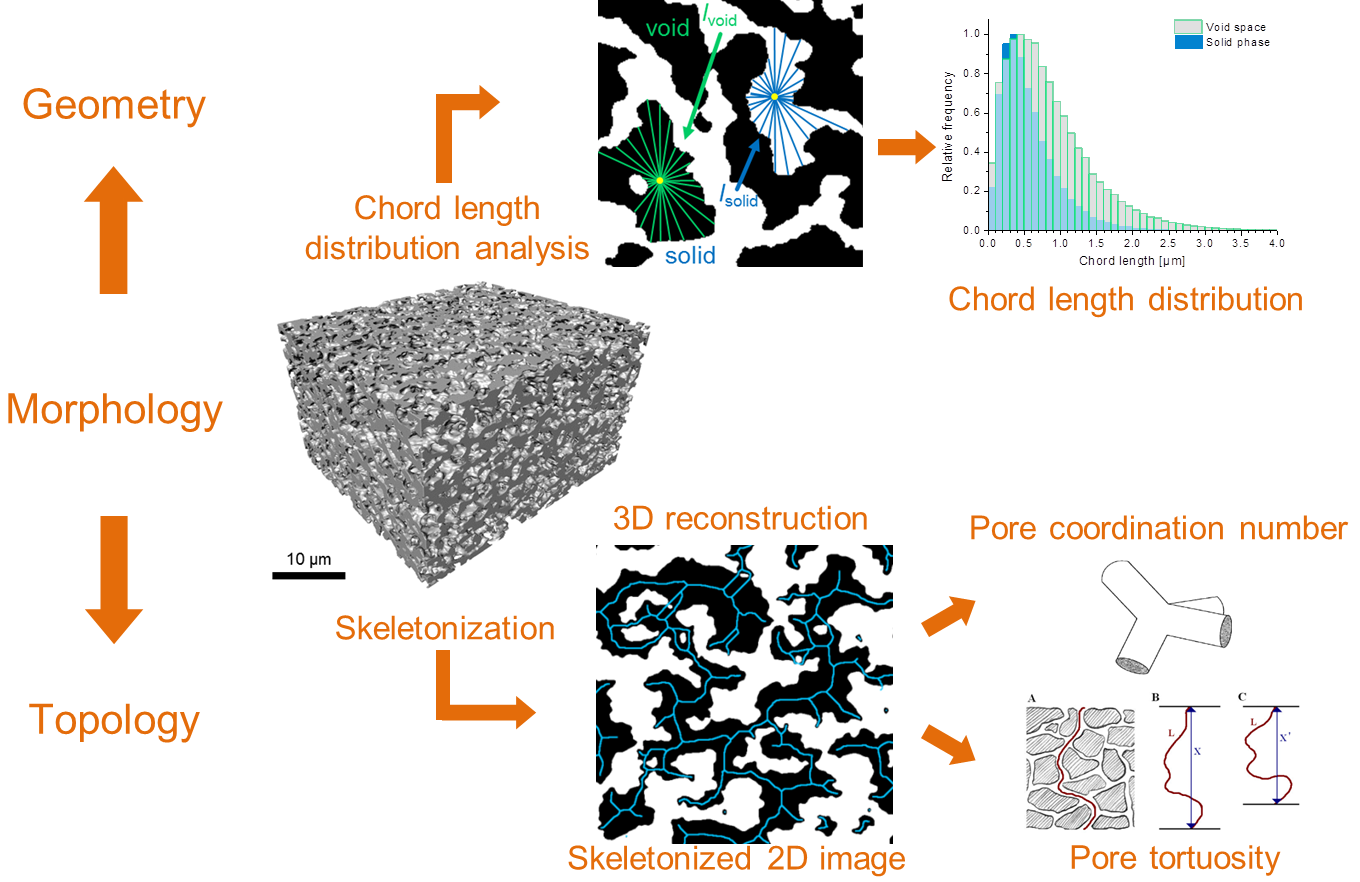
Figure 6: Schematic illustration of the quantitative analysis of porous materials (courtesy Dr. Daniela Stöckel, University Marburg)
Application areas for the research include separation media such as silica monolith used in HPLC, where we could correlate the average pore diameter in these disordered materials with the structural uniformity (Fig. 7) and catalysis, where the pore structure (Fig. 8) is influencing the catalytic performance and selectivity.
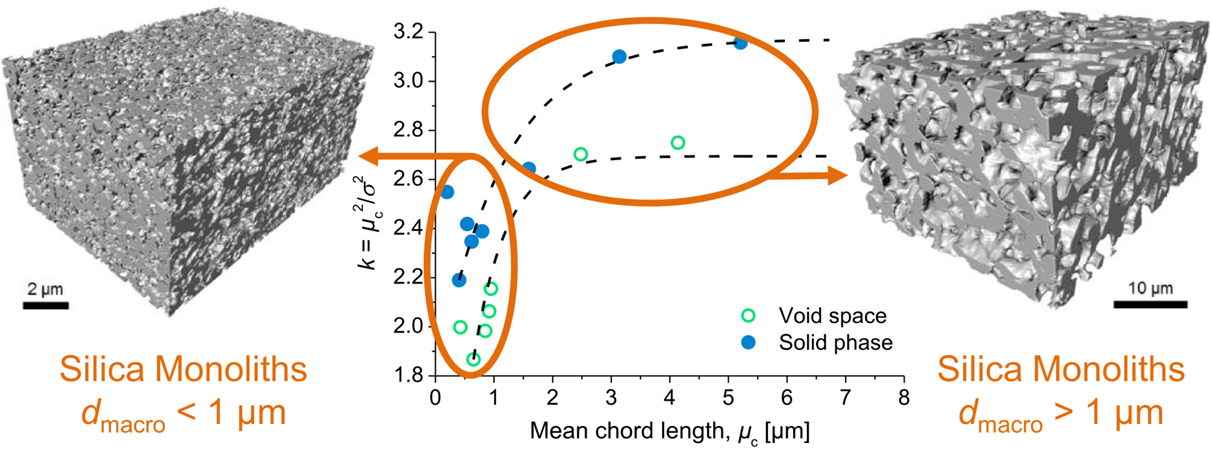
Figue 7: Quantitative analysis of a series of FIB slice&view tomography reconstructions of silica monoliths with different pore sizes: The order parameter k is uniform when the average pore diameter (represented by the mean chord length) is larger than ~ 1 um, but decreases rapidly for smaller average pore sizes.
D. Stoeckel, C. Kübel, M. Loeh, B. Smarsly, U. Tallarek, Langmuir, 2015, 31(26), 7391–7400; DOI: 10.1021/la5046018.
|
|
|
|
|
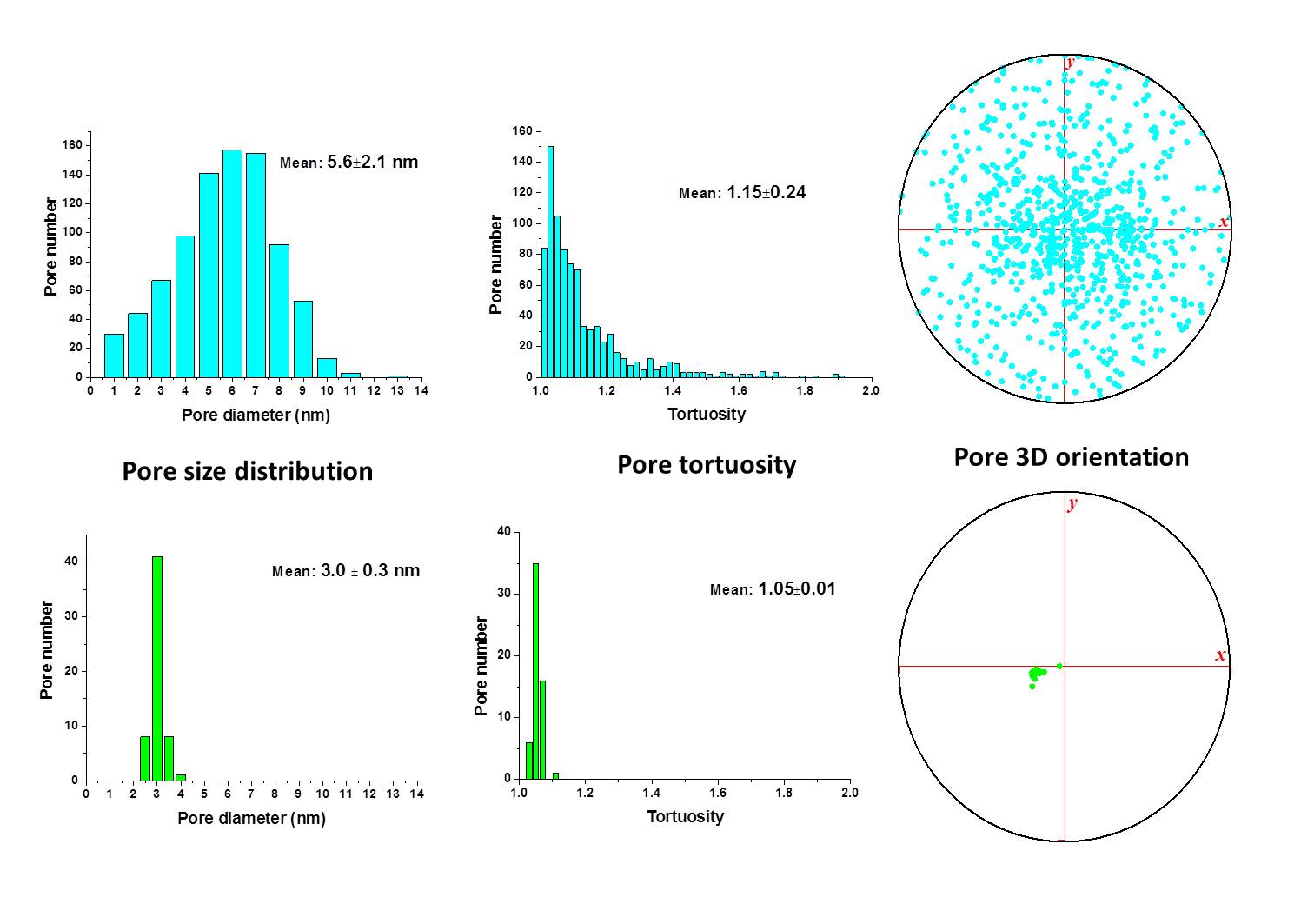
Figure 8: Segmented 3D reconstruction of a disordered and an ordered mesoporous carbon with a quantitative analysis of the pore size distributionand, the tortuosity and the pore orientation (pole figure) providing a quantitative description of the visually intuitive differences between the materials.
Reconstruction Artefacts
The quality and reliability of the 3D reconstruction depends crucially on
1) the quality of the input images
2) the alignment accuracy
3) angular sampling and coverage
4) the reconstruction algorithm
Alignment
The artifacts introduced by a limited alignment accuracy can be best understood based on the real space backprojection representation of the reconstruction process. Shifts between images in the tilt-series lead to a smearing of the reconstructed object. In particular, if the tilt-axis position is offset, this results in the so called 'banana shape' of small reconstucted features (Fig. 9b). Furthermore, if the images are systematically shifted in one direction from one image to the next in the tilt-series (which often happens with a cross-correlation alignment), this results in a 'Mercedes star' type structure for small features (Fig. 9c)

Fig. 9: Alignment artifacts visible in the XZ plane of a 3D reconstruction: a) well-aligned symmetric missing wedge artifacts due to limited tilt-range (strongly enhanced for visibility), b) offset of the tilt-axis position (5 pixels) leading to banana shaped streaks and c) continuous shift between images in the tilt-series of 0.1 pixel result in a 'Mercedes star' shape.
Missing Wedge and Angular Sampling
The effects of angular sampling and coverage on the 3D reconstruction can best be visualized in recipical space. If one considers the Fourier synthesis of the 3D object by combining the Fourier transforms of the images obtained at all different tilt-angles, it becomes immidiately visible that a limited tilt-range during the acquisition results in a missing wedge of information in the 3D Fourier space. Any Fourier coefficients of the original object in this missing wedge will not be reconstructed and thus not be visible in the 3D reconstruction. Furthermore, a large angular increment will results in a poor resolution in 3D as the 3D sampling becomes coarse.

Fig. 10: Schematic representation of the missing wedge and limited angular sampling.
Reconstruction Algorithms
The Fourier sampling at low spatial frequencies is much higher compared to the sampling at low spatial frequencies. Therefore, a stright backprojection would result in an overestimate of the low frequencies while the high frequencies are underestimated, leading to a very blurry reconstruction.
One approach commonly used to overcome this problem is weighted backprojection (WBPJ), where a weighting filter is introduced reducing the contribution of the low spatial frequencies (Fig. 11).

Fig. 11: Comparison of straight backprojection (BPJ) and weighted backprojection (WBPJ).
Alternatively, iterative approaches such as the Simultaneous Iterative Reconstruction Technique (SIRT) are nowadays commonly used in materials sciences. In addition to reducing the oversampling, the SIRT approach also reduces the noise in the reconstruction compared to WBPJ.
However, with both reconstruction approaches, it is difficult to accurately reconstruct the object intensities in 3D. The exact shape of the weighting filter (a Fourier filter) introduces strong artifacts for the intensities. In the example of a zirconia filled polymer shown in Fig. 12, this effect can be seen as the image intensity of the vacuum around the sample is almost identical to the intensity of the polymer matrix. In the SIRT reconstruction of the same data set, the relative intensities are better preserved.

Fig. 12: Electron tomographic reconstruction of zironia nanoparticles in a polymer matrix: comparison of WBPJ and SIRT and missing wedge effect (N. Kawase, M. Kato, H. Nishioka, H. Jinnai, Ultramicroscopy, 2007, 107, 8-15).
However, also the SIRT reconstruction does not produce easily quantifiable intensities that can be directly segmented by thresholding. Because of convergence limitations, there is a dependence of the reconstructed intensities of the averge density overlapping in the different projections. As one example, when reconstructing nanoparticles with different diameter, this results in decreasing intensities with decreasing particle diameter, which makes an accurate segmentation very difficult.

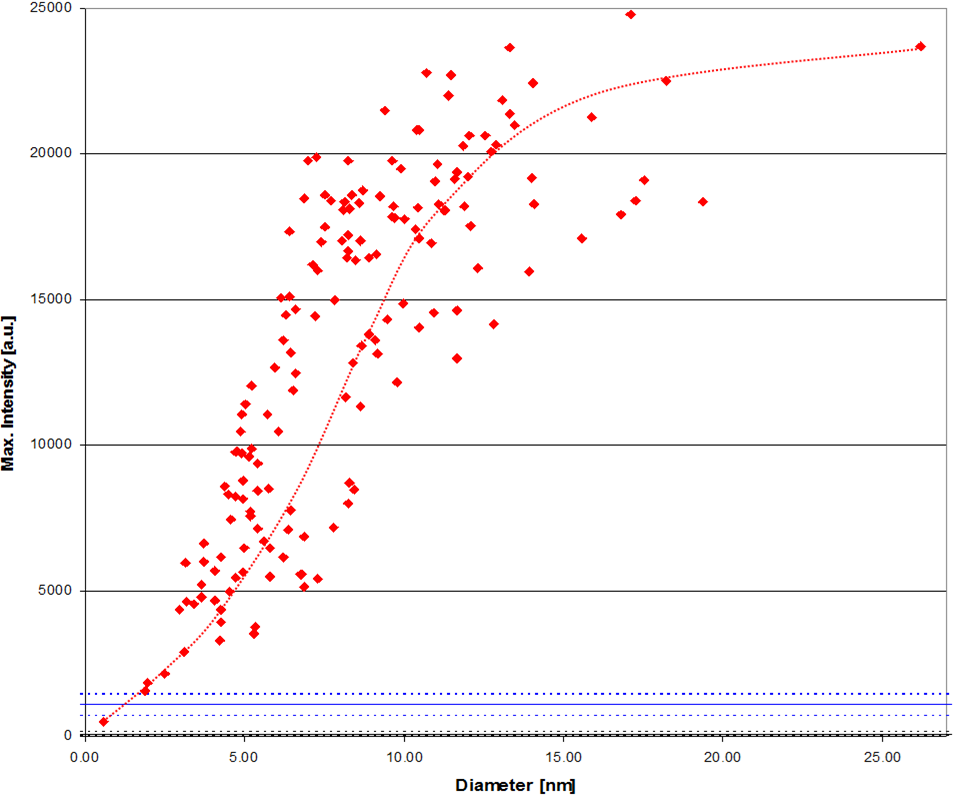
Fig. 13: 3D reconstruction of metal nanoparticles on a catalyst support. The graph shows the experimental correlation between particle size and reconstructed average intensity of the particles (from C. Kübel, D. Niemeyer, R. Cieslinski, S. Rozeveld, J. Mat. Sci. Forum, 2010, 638-642, 2517-2522).
Currently, a number of alternative techniques such as discrete tomography or compressive sensing are being develop to overcome these limitations when the sample fulfills appropriate requirements.